Bài tập hình học cải thiện Toán 7 là tài liệu luyện thi chẳng thể thiếu dành cho các học viên tham khảo. Tài liệu thể hiện chi tiết trọng tâm những dạng bài tập hình học 7, giúp học viên có phương hướng ôn thi đúng chuẩn nhất.
Bạn đang xem: Các bài toán nâng cao lớp 7 hình học
Bài tập Hình học nâng cấp lớp 7 được soạn theo các chủ đề trọng tâm, khoa học, tương xứng với mọi đối tượng học sinh có học lực từ bỏ khá đến giỏi. Thông qua đó giúp học sinh củng cố, nắm bền vững kiến thức nền tảng, áp dụng với các bài tập cơ bản; học sinh có học tập lực khá, giỏi cải thiện tư duy và năng lực giải đề với các bài tập áp dụng nâng cao. Vậy sau đấy là bài tập nâng cấp Hình học tập 7, mời các bạn cùng quan sát và theo dõi tại đây.
Bài tập nâng cấp Hình học tập 7
I. Bài tập từ luyện
Bài toán 1. mang đến ΔABC vuông cân nặng tại A, trung đường AM. Lấy E ∈ BC. BH, chồng ⊥ AE (H, K ∈ AE). Chứng tỏ rằng Δ MHK vuông cân.
Bài toán 2. mang lại ΔABC tất cả góc ABC = 500; góc BAC = 700. Phân giác trong góc acb cắt AB trên M. Trên MC lấy điểm N sao để cho góc MBN = 400. Minh chứng rằng: BN = MC.
Bài toán 3. Cho ΔABC. Vẽ ra phía kế bên của tam giác này các tam giác vuông cân ở A là ABE và ACF. Vẽ AH ⊥ BC. Đường trực tiếp AH giảm EF trên O. Minh chứng rằng O là trung điểm của EF.
Bài toán 4. cho ABC. Qua A vẽ mặt đường thẳng xy // BC. Từ bỏ điểm M bên trên cạnh BC vẽ những đường thẳng tuy vậy song với AB, AC chúng giảm xy theo thứ tự trên D và E. Chứng tỏ rằng:
a. ΔABC = ΔMDE
b. Ba đường trực tiếp AM, BD, CE thuộc đi qua một điểm.
Bài toán 5. mang lại ABC vuông tại A. Bên trên cạnh BC lấy hai điểm M cùng N làm sao để cho BM = BA; cn = CA. Tính góc MAN
Bài toán 6. Cho đoạn trực tiếp MN = 4cm, điểm O nằm trong lòng M và N. Trên cùng một nửa mặt phẳng bờ MN vẽ những tam giác cân nặng đỉnh O là OMA với OMB làm sao để cho góc sống đỉnh O bởi 450. Tìm địa điểm của O để AB min. Tính độ dài nhỏ tuổi nhất đó.
II. Bài tập gồm đáp án
BÀI 1: đến ∆ABC nhọn. Vẽ về phía ngoại trừ ∆ABC các ∆ rất nhiều ABD với ACE. Hotline M là giao điểm của BE với CD. Chứng minh rằng:
a) ∆ABE = ∆ADC
b) Góc BMC = 120o
Bài 2: mang lại tam giác ABC có bố góc nhọn, mặt đường cao AH. Làm việc miền ko kể của tam giác ABC ta vẽ những tam giác vuông cân ABE và ACF phần nhiều nhận A có tác dụng đỉnh góc vuông. Kẻ EM, FN thuộc vuông góc cùng với AH (M, N thuộc AH).
a) chứng minh: EM + HC = NH.
b) triệu chứng minh: EN // FM.
Bài 3: Cho cạnh hình vuông vắn ABCD có độ lâu năm là 1. Trên các cạnh AB, AD lấy những điểm P, Q làm sao cho chu vi DAPQ bởi 2.
Chứng minh rằng : Góc PCQ = 45o
Bài 4: Cho tam giác vuông cân ABC (AB = AC), tia phân giác của những góc B với C giảm AC cùng AB thứu tự tại E cùng D.
a) minh chứng rằng: BE = CD; AD = AE.
b) hotline I là giao điểm của BE cùng CD. AI giảm BC sống M, chứng tỏ rằng những ∆MAB; MAC là tam giác vuông cân.
c) từ bỏ A với D vẽ những đường trực tiếp vuông góc cùng với BE, các đường trực tiếp này giảm BC lần lượt sống K với H. Chứng minh rằng KH = KC.
Bài 5: cho tam giác cân nặng ABC (AB = AC ). Bên trên cạnh BC lấy điểm D, bên trên tia đối của tia CB rước điểm E làm thế nào cho BD = CE. Những đường thẳng vuông góc với BC kẻ trường đoản cú D và E cắt AB, AC lần lượt ở M, N. Chứng minh rằng:
a) DM = EN
b) Đường trực tiếp BC cắt MN tại trung điểm I của MN.
c) Đường trực tiếp vuông góc cùng với MN trên I luôn luôn đi sang một điểm thắt chặt và cố định khi D chuyển đổi trên cạnh BC.
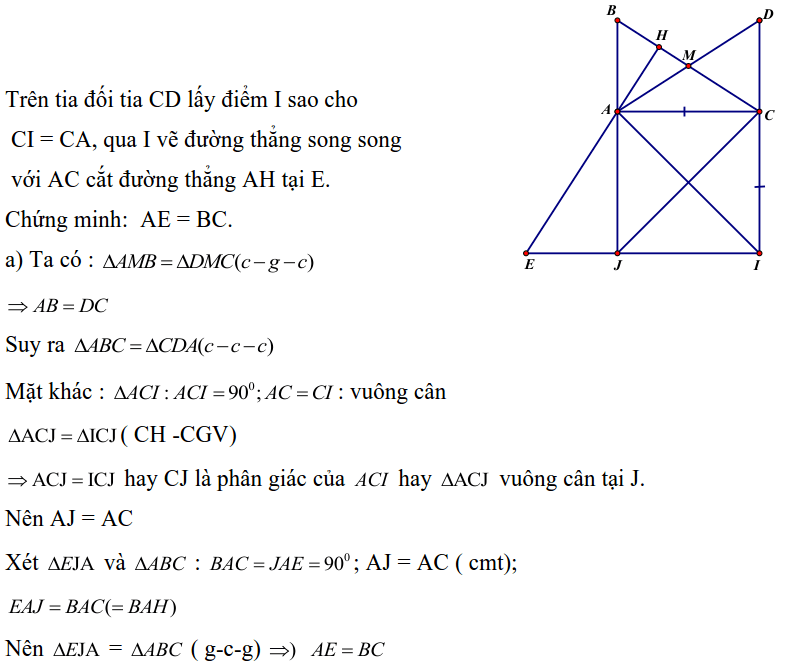
Bài 6: Cho tam giác vuông ABC: A = 90o , mặt đường cao AH, trung con đường AM. Trên tia đối tia MA đem điểm D thế nào cho DM = MA. Bên trên tia đối tia CD rước điểm I sao cho
CI = CA, qua I vẽ con đường thẳng tuy nhiên song cùng với AC cắt đường trực tiếp AH tại E.
Xem thêm: Trà thảo mộc cô đặc herbalife tea concentrate, tpbvsk: trà thảo mộc cô đặc
Chứng minh: AE = BC.
Bài 7: Cho cha điểm B, H, C thẳng hàng, BC = 13 cm, bảo hành = 4 cm, HC = 9 cm. Từ bỏ H vẽ tia Hx vuông góc với con đường thẳng BC.
Lấy A nằm trong tia Hx làm thế nào để cho HA = 6 cm.
a) ∆ABC là ∆ gì ? chứng tỏ điều đó.
b) bên trên tia HC lấy điểm D làm thế nào cho HD = HA. Từ bỏ D vẽ đường thẳng song song với AH giảm AC tại bệnh minh: AE = AB
Bài 8: Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của của tia MA lấy điểm E làm sao để cho ME = MA. Minh chứng rằng:
a) AC = EB cùng AC // BE
b) gọi I là một trong điểm trên AC ; K là 1 trong điểm trên EB thế nào cho AI = EK . Chứng minh ba điểm I , M , K trực tiếp hàng
c) từ bỏ E kẻ EH ⊥ BC (H ∈ BC). Biết góc HBE = 50o ; góc MEB = 25o. Tính goc HEM cùng góc BEM.
Bài 9: Cho tam giác ABC cân nặng tại A bao gồm A = 20o, vẽ tam giác đa số DBC (D phía trong tam giác ABC). Tia phân giác của góc ABD giảm AC tại M. Hội chứng minh:
a) Tia AD là phân giác của góc BAC b) AM = BC
Bài 10: Cho hình vuông vắn ABCD, điểm E nằm trong cạnh CD. Tia phân giác của góc ABE giảm AD sinh sống K. Chứng tỏ AK + CE = BE.
Tăng cường khả năng giải Toán Hình học cho học sinh lớp 7 với 10 bài tập hình học cải thiện có lời giải được Gia sư Tiến Bộ chia sẻ dưới đây.
BÀI 1: cho ∆ABC nhọn. Vẽ về phía ngoài ∆ABC các ∆ đều ABD cùng ACE. Gọi M là giao điểm của BE cùng CD. Chứng minh rằng:
a) ∆ABE = ∆ADC
b)
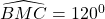
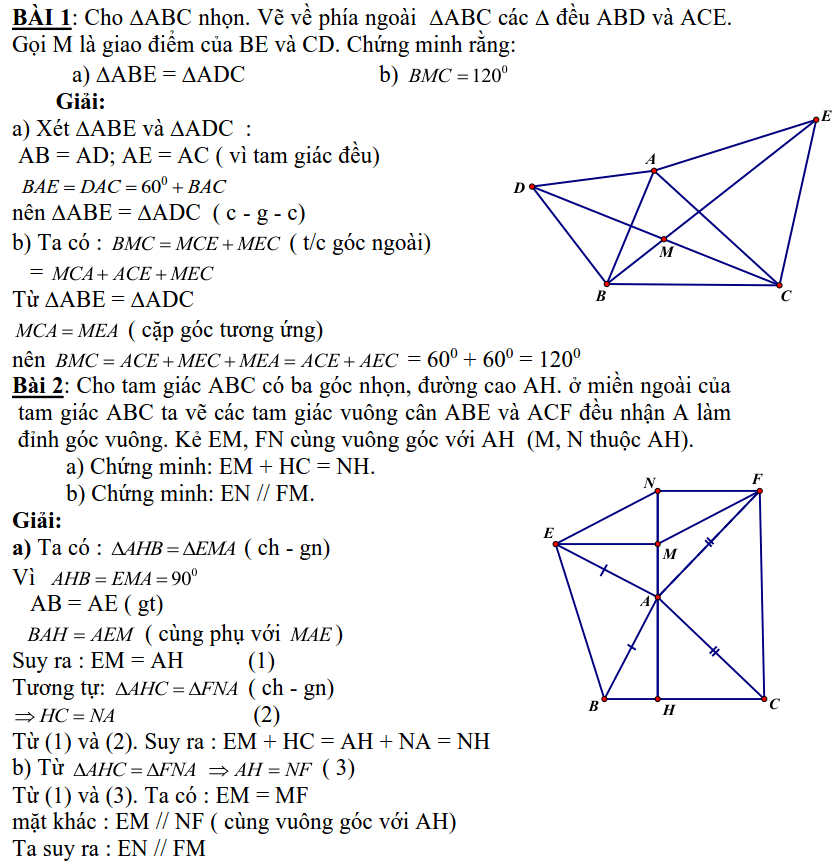
Bài 2: mang đến tam giác ABC có tía góc nhọn, đường cao AH. ở miền ngoại trừ của tam giác ABC ta vẽ các tam giác vuông cân ABE cùng ACF đều nhận A có tác dụng đỉnh góc vuông. Kẻ EM, FN thuộc vuông góc với AH (M, N thuộc AH).
a) Chứng minh: EM + HC = NH.
b) Chứng minh: EN // FM.
Bài 3:Cho cạnh hình vuông vắn ABCD có độ dài là 1. Trên các cạnh AB, AD lấy các điểm P, Q sao cho chu vi DAPQ bằng 2.
Chứng minh rằng :
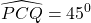
Bài 4:Cho tam giác vuông cân nặng ABC (AB = AC), tia phân giác của các góc B và C cắt AC với AB lần lượt tại E và D.
a) Chứng minh rằng: BE = CD; AD = AE.
b) Gọi I là giao điểm của BE và CD. AI cắt BC ở M, chứng minh rằng những DMAB; MAC là tam giác vuông cân.
c) Từ A cùng D vẽ các đường thẳng vuông góc với BE, các đường thẳng này cắt BC lần lượt ở K và H. Chứng minh rằng KH = KC.
Bài 5: đến tam giác cân ABC (AB = AC ). Trên cạnh BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Các đường thẳng vuông góc với BC kẻ từ D cùng E cắt AB, AC lần lượt ở M, N. Chứng minh rằng:
a) DM = EN
b) Đường thẳng BC cắt MN tại trung điểm I của MN.
c) Đường thẳng vuông góc với MN tại I luôn đi qua một điểm cố định khi D chũm đổi trên cạnh BC.Bài 6: cho tam giác vuông ABC:
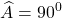
Bài 7: Cho tía điểm B, H, C thẳng hàng, BC = 13 cm, bảo hành = 4 cm, HC = 9 cm. Từ H vẽ tia Hx vuông góc với đường thẳng BC. Lấy A thuộc tia Hx làm thế nào cho HA = 6 cm.
a) ∆ABC là ∆ gì ? Chứng minh điều đó.
b) bên trên tia HC lấy điểm D sao để cho HD = HA. Từ D vẽ đường thẳng tuy vậy song với AH cắt AC tại Chứng minh: AE = AB
Bài 8: Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của của tia MA lấy điểm E làm sao cho ME = MA. Chứng minh rằng:
a) AC = EB và

b) Gọi I là một điểm trên AC ; K là một điểm bên trên EB thế nào cho AI = EK . Chứng minh ba điểm I , M , K thẳng hàng
c) Từ E kẻ

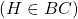
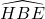
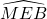
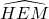
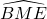
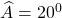
a) Tia AD là phân giác của góc BAC b) AM = BCBài 10: Cho hình vuông ABCD, điểm E thuộc cạnh CD. Tia phân giác của góc ABE cắt AD ở K. Chứng minh AK + CE = BE.
Đáp án


Bài tập nâng cấp và một số chuyên đề Toán 7 – Bùi Văn Tuyên >>









